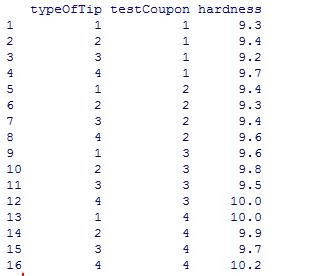
The test data is
Let us look at the interaction plot
and the box plot
Let us now run the analysis of variance on the data, we will include the blocking variable in the analysis.
the formula to be used in R is hardness~typeOfTip+testCoupon.
> anova(aov(hardness~factor(typeOfTip)+factor(testCoupon)))
Analysis of Variance Table

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
A plot of the residuals should not show any pattern since the residuals are assumed to be independently distributed for analysis of variance. Here’s the plot of the residuals.
A Quantil-Quantile plot can be used to check the distribution as well. The plot also shows the presence of outliers, if any. The plot is shown below.
Tukeys test can be used for pairwise comparison. Here’s the result of the Tukey’s test
fit=aov(hardness~factor(typeOfTip)+factor(testCoupon))
TukeyHSD(fit,which=’factor(typeOfTip)’,ordered=”TRUE”)
A plot of the residuals should not have a pattern. Here’s a plot of the residuals.
We can check for variance. Here’s a method to check to equality of variance.
> summary(lm(abs(fit$res)~typeOfTip))
Call:
lm(formula = abs(fit$res) ~ typeOfTip)
Residuals:
Min 1Q Median 3Q Max
-0.050000 -0.032812 -0.003125 0.026562 0.093750
Coefficients:
Estimate Std. Error t value Pr(>t)
(Intercept) 0.075000 0.024719 3.034 0.00893 **
typeOfTip -0.006250 0.009026 -0.692 0.50000
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.04037 on 14 degrees of freedom
Multiple R-squared: 0.03311, Adjusted R-squared: -0.03595
F-statistic: 0.4795 on 1 and 14 DF, p-value: 0.5
Since the p-value is large, difference in variance cannot be stated.
The Latin Square Design:
If there are two blocking variables then the latin square design can be used.
problem : Suppose that an experimenter is studying the effects of five different formulations of a rocket propellant used in aircrew escape systems on the observed burning rate. Each formulation is mixed from a batch of raw material that is only large enough for five formulations to be tested. Furthermore, the formulations are prepared by several operators, and there may be substantial differences in the skills and experience of the operators.
Here’s the data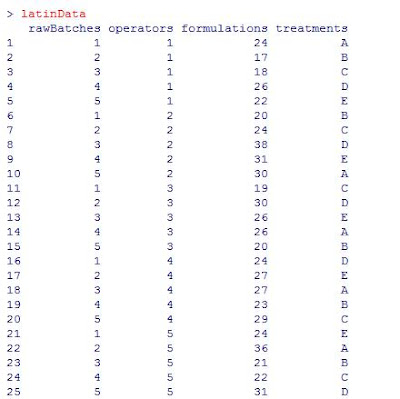
The latin square structure is
> matrix(treatments,5,5)
[,1] [,2] [,3] [,4] [,5]
[1,] “A” “B” “C” “D” “E”
[2,] “B” “C” “D” “E” “A”
[3,] “C” “D” “E” “A” “B”
[4,] “D” “E” “A” “B” “C”
[5,] “E” “A” “B” “C” “D”
An analysis of variance gives
> anova(lm(formulations~factor(rawBatches)+factor(treatments)+factor(operators)))
The data shows that the different formulations do produce different burning rate. Also there is a difference between the operators. However, no difference between the raw batches.