R is a powerful language for statistical computing and graphics. R has a strong community support and is finding new use in the corporate world. If R can be integrated with Java, it would provide a greap acceptance into new products. A library called rjava exists that helps integrate R with Java. However, setting up the library may be tricky.
This post explores how R can be called from within Java using JRI. We will use the example provided in the rjava package. The example class is called rtest2.java.
Here are the steps to run R from java using eclipse.
1) Create a new project and copy the rtest.java and rtest2.java files from the rjava/jri package. The rjava project folder can be found at the place where R stores the package downloaded during the install step. It should be in a folder called ‘win-library’.
2) the rjava/jri folder in ‘win-library’ should also have the JRI.jar library and jri.dll file. copy R.dll from the bin directory of R into the rjava/jri folder.
Here’s the folder hierarchy for JRI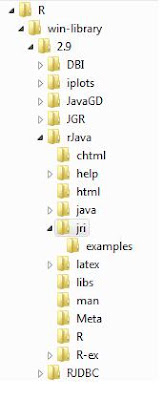
3) add the JRI.jar in the project classpath in eclipse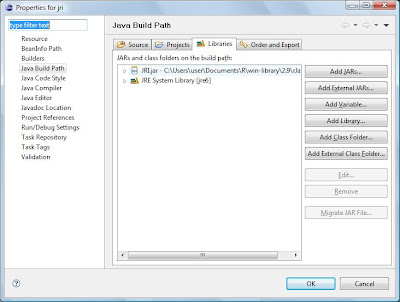
4) Add the following entries into the run configuration of the product.
THe path variable contains
C:/Users/user/Documents/R/win-library/2.9/rJava/jri/;C:Program FilesRR-2.9.1bin
That’s it. This should work. Run the rtest2 file and you should see R working.
Some of the steps above may not be required. However, i have found this to be working after some research and would not like to experiment further. Please add your comments if it works and also if it does not.

thanks for the great tutorial!
I’m working with netbeans, so it isn’t realy the same. Could you help with this?
Hi marc. If you still need help with netbeans, let me know, i will try it in netbeans and update this post.
Hi Mithil, before I set up R-Java in eclipse, I wanted to ask one thing. Is it as good as using stand-alone R. Can I use packages in R and draw plots with ease?
Hi Yogesh,
If your problem can be solved by using stand alone R then that would work better. R-Java would be helpful only in case you want to call R from your java application. For graphs, the way i do it is use a jpeg output type instead of the default type in R. all plots are then created as jpeg files. you can then use this jpeg files in your java/web application.
Also currently there is no way to access R via multithreaded java. so you would have to create multiple R instances from your java code and then use a thread pool to fire requests to R from java.
Everytime your fire a request, the R datatype is converted to a java object and returned back, so there is an overhead
Hi Mithil,
Thanks for this post. However its still not working for me. When I try to run rtest2.java i always get “Cannot find JRI native library!
Please make sure that the JRI native library is in a directory listed in java.library.path.” Do I need to set in the classpath on the jri.jar the native libraries manually? And if so what is the directory? I did everything as you told in the post. Hope you can help me.
bye
And thanks
Richard
Hi Richard,
Here’s what you need to double check:
1. have you set up the path to the bin directory of R correctly in the run configuration.
2. Have you set up the path to the rJava jri directory correctly in the run configuration.
3. Is R and Java installed properly.
4. jri.jar should be in the build path of the eclipse project (if the project compiles properly, then you are good).
If it still fails send me the screenshot of the run configuration and the eclipse project and i will take a look at it.
Hi thus article is great!
Thank you brother.
It helped me solving the native library problem when using Java, R and Eclipse
Bye
thanks for tutorial,
give me some example code to call rfunctions….
Hi Mithil,
Very helpful document. I ran rtest2.java no error. But little confuse about what it is supposed to do.
Press to continue (time to attach the debugger if necessary)
— I pressed enter, then it shows the message
Creating Rengine (with arguments)
after that nothing happens.
Same way, I ran rtest.java but getting error
Cannot find JRI native library!
Please make sure that the JRI native library is in a directory listed in java.library.path.
java.lang.UnsatisfiedLinkError: C:UsersrbhaumikDocumentsRwin-library2.9rJavajrijri.dll: Can’t find dependent libraries
at java.lang.ClassLoader$NativeLibrary.load(Native Method)
at java.lang.ClassLoader.loadLibrary0(Unknown Source)
at java.lang.ClassLoader.loadLibrary(Unknown Source)
at java.lang.Runtime.loadLibrary0(Unknown Source)
at java.lang.System.loadLibrary(Unknown Source)
at org.rosuda.JRI.Rengine.(Rengine.java:19)
at rtest.main(rtest.java:62)
would you please help me
hi mithil,
give me some example code inorder to call database from r tool and do some analysis on data.
hi mithil,
give me some example r fcode for cconnecting database and do some analysis on data.
This comment has been removed by the author.
Thank you for your great tutorial !
Hello again,
everything’s ok when I launch my application wich create a Rengine but when I try to evaluate something with R, a fatal error occurs :
#
# A fatal error has been detected by the Java Runtime Environment:
#
# EXCEPTION_ACCESS_VIOLATION (0xc0000005) at pc=0x6c731a9e, pid=3708, tid=2420
#
# JRE version: 6.0_24-b07
# Java VM: Java HotSpot(TM) Client VM (19.1-b02 mixed mode, sharing windows-x86 )
# Problematic frame:
# C [R.dll+0x31a9e]
The error seems to come from the access to R.dll …
Thanks for your help if you have time to handle this.
Hi! how are you? I have a problem when I’m trying to compile. This is the error:
Cannot find JRI native library!
Please make sure that the JRI native library is in a directory listed in java.library.path.
java.lang.UnsatisfiedLinkError: C:WindowsSystem32jri.dll: Can’t find dependent libraries
It is similar with the other post but in this case to point to System32. I’m using Windows 7 and I have already runned eclipse as Administrator and it doesn’t work. Could you help me please?
Oh! and I have already copied the file jri.dll in System32
Everyone gets the problem looks like
“Cannot find JRI native library!
Please make sure that the JRI native library is in a directory listed in java.library.path.”
should try the way below. It’s a entry mithil wrote for 64-bit machines.
http://mithil-tech.blogspot.com/2011/04/r-and-java-installing-rjava-on-64-bit.html
You should set up the Run Configurations like the comment of Yoichi. It’s exactly what you need.
Thank you the great tutorial also from me, Mithil.
Everything you described works perfectly (I can transfer data from Java to R and back after a calculation).
Now I have a another problem:
I want to use R in a Webstart application and therefore I want to integrate the complete R into my war file.
So far I understand JRI needs an installation of R in the C:Program FilesR… directory.
Is it possible to integrate all necessary files from the C:Program FilesR… directory in my WebStart application? And how can I do that?
Thank you very much for you effort!
Greetings,
Daniel
I found a better way to integrate my math function into my Webstart application:
Apache Common Math Libraries.
Plz can you tell me how to integrate the java to r using Rserve.I need to pass Result set of query to R console..Plz send me the sample code..
Hi mithil, followed the steps but still getting the error – Cannot find JRI native library!
Hi mithil, followed the steps but still getting the error – Cannot find JRI native library!
why nobody tells that how they found a solution to this problem?
please tell us how you figured out to get rid of this error
You need to make sure that java home is in path. or try and add the path in the eclipse run environment. mail me if you still cant make it run. The others in the post above were able to run it eventually.
For Concurrent systems; this approach wouldnt work efficiently.
rForge suggest us to use RServe, now i have a question on this?
FAQ of RServe Says:
How to start Rserve?
One way to start Rserve is from within R, just type
library(Rserve)
Rserve()
So primarily we can pass command RServe() via JRI once and it would instante RServer for us. For all other communication we can then start using Rserve pure java TCP/IP calls with out worring much about the memory leaks n other java2R communication issues.
big question ? is my above assumption correct
the documentation says it(Rserve) doesnt support concurrency or multi threaded feature as on unix, so let me move to apache maths! Sorry folks R is not helping me much.
Txs a lot. Spent like 10hs to get this to work. It would have taken 10mins if I accessed your post. Rgds
Thanks a lot. Its working!
I also had the UnsatisfiedLinkError, saying it can not find the dll at location x, despite the dll being there.
For me, this was a wrong error message, because the problem wasn’t with the jri.dll, but with the R bin location.
In my R Version, the binaries are not located at:
C:Program FilesRR-2.15.2bin
but in:
C:Program FilesRR-2.15.2bini386
After I corrected the path, the error with the jri.dll disappeared.
However that damn faulty error message did still cost me a lot of time. 🙁
Hi mithil,
Thanks for the tutorial
when i run rtest2 with netbeans i have an interface containing this messeges: R version 2.15.2 (2012-10-26) — “Trick or Treat”
Copyright (C) 2012 The R Foundation for Statistical Computing
ISBN 3-900051-07-0
Platform: i386-w64-mingw32/i386 (32-bit)
R est un logiciel libre livré sans AUCUNE GARANTIE.
Vous pouvez le redistribuer sous certaines conditions.
Tapez ‘license()’ ou ‘licence()’ pour plus de détails.
R est un projet collaboratif avec de nombreux contributeurs.
Tapez ‘contributors()’ pour plus d’information et
‘citation()’ pour la façon de le citer dans les publications.
Tapez ‘demo()’ pour des démonstrations, ‘help()’ pour l’aide
en ligne ou ‘help.start()’ pour obtenir l’aide au format HTML.
Tapez ‘q()’ pour quitter R.
Letting go; use main loop from now on
but i don’t know how to execute my rscript!!
Can u give me an exemple how to run an rscript please??
when i run rthis test2 i have this message in netbeans output : Press to continue (time to attach the debugger if necessary)
Creating Rengine (with arguments)
Rengine created, waiting for R
re-routing stdout/err into R console
rBusy(0)
>
i don’t interstand what it mean can help me to resolve this and runing an Rscript via java please
Hi,
There are two ways to run java from R. either open an R console (that is what test2) does or directly run R code from java (which is what you want to do) Look at the test.java example in rJavajriexamples. Also the tutorial at http://www.studytrails.com/RJava-Eclipse-Plugin/Execute-R-From-Java.jsp explains more.
thaank you mithil
i use rtest2 my problem now is that when the r console is visible i can’t write my code dirctly in this Rconsole but i must write it in the netbeans output
“Creating Rengine (with arguments)” what arguments are required here. Both the programs rtest and rtest2 terminate after i get the message as shown above.
Kindly ignore the comments. R_HOME was not set even though I had copied R.dll in jri folder, it wasnt enough.
I followed all the steps but Java terminates on this statement
Rengine re=new Rengine(args, false, new TextConsole());
On further debugging I see that I get a core dump from the Java native libraries. What could be wrong in my case ?